Set Theory

Set Theory

        A Set is a collection of objects, things, or states. The Objects may be numbers, letters, days of the week, or in fact, anything under discussion. One way of describing a set is to list the whole collection of members or elements and enclose them in braces { }.

               Ex: A.{1, 0} the set of binary digits, one and zero

                      B.{off, on} the set of possible states of a two-state system

 Equal Set

       Two sets are said to be equal if they contain exactly the same members or elements.

              Ex: A.{2, 5, 9}

                     B.{5, 9, 2}

        They are both equal to each other. The order in which we write down the elements is immaterial.

If you have a set like this {2, 2, 5, 9} and {2, 5, 9} they both are equal because the repetition of elements is ignored.

Venn Diagrams

As you can see in the Picture the element of number in the 5x table are {5, 10, 25} and the elements of the Odd numbers are {5, 25, 31}.

In the middle there are 5 and 25 those elements are common to both sets.

There some law for the Venn Diagrams. These Laws are shown below:

The Commutative Laws

The Associative Laws

The Distributive Laws

The Identity Laws

The Complement laws

The Absorption Laws

The Minimization Law

De Morgan's Laws

Exercise For Set Theory

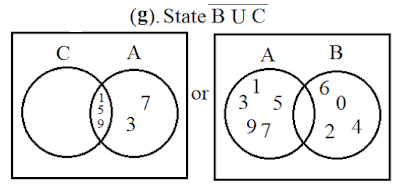
          I. The Set A, B, and C are given by 

                A.{1, 3, 5, 7, 9}

                B.{0, 2, 4, 6}

                C.{1, 5, 9}

                E.{0, 1, 2, 3, 4, 5, 6, 7, 8, 9,}(The Universal set)

           

(a). Represent the sets on a Venn Diagram.

          II. Use Venn Diagrams to illustrate the following for general sets C and D

          III. By Drawing Venn Diagrams verify De Morgan's Laws

That all for the Set Theory Hope it helps you to some extent. Good-Bye